递归算法系统化总结

前言

大家都听说过这个故事吧：从前有座山，山里有座庙，庙里有个老和尚，老和尚在给小和尚讲故事：从前有座山，山里有座庙，庙里有个老和尚，老和尚在给小和尚讲故事：从前有座山…

这是一个不断循环的故事， 一般用于哄小宝宝睡觉前讲的。这个有趣的故事就蕴含了递归的思想。对于递归，我们总是惊叹于它用来描述问题的能力和编写代码的简洁，但要想真正领悟递归的精髓、灵活地运用递归思想来解决问题却并不是一件容易的事情。本文的目的就是理清递归的知识脉络，方便初学者建立一个系统化的知识架构。

1、什么是递归？

递归的英文是：Recursion，起源于数学。在数学中，递归是指在函数的定义中使用函数自身的方法。如下面等差数列的定义：

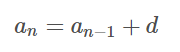
递归函数的字面定义很简单，但是在计算过程中则变得十分复杂。在计算机科学中，递归，顾名思义，其包含了两个意思：“递” 和 “归”，这正是递归思想的精华所在。

递归就是有去有回，“有去”是指，递归问题必须可以分解为若干个规模较小，与原问题形式相同的子问题，这些子问题可以用相同的解题思路来解决；“有回”是指 :，这些问题的演化过程是一个从大到小，由近及远的过程，并且会有一个明确的终点(临界点)，一旦到达了这个临界点，就不用再往更小、更远的地方走下去。最后，从这个临界点开始，原路返回到原点，原问题解决。关于“有去有回”的直接感受，请看下文关于阶乘的求解。一直钻入f(1)为止，然后原路返回，最后获得计算结果。

递归的精髓就是把规模大的问题转化为规模小的相似的子问题来解决。特别地，在函数实现时，因为解决大问题的方法和解决小问题的方法往往是同一个方法，所以就产生了函数调用它自身的情况，这也正是递归的定义所在。格外重要的是，这个解决问题的函数必须有明确的结束条件，否则就会导致无限递归的情况。

2、递归三要素是什么？

在我们了解了递归的基本思想之后，我们如何才能写出一个漂亮的递归程序呢？主要是把握以下三个方面：

（1）明确递归终止条件。如上文所示，递归就是有去有回，既然这样，那么必然应该有一个明确的临界点，程序一旦到达了这个临界点，就不用继续往下递去而是开始实实在在的归来。换句话说，该临界点就是一种简单情境，可以防止无限递归。

（2）给出递归终止时的处理办法。 实际上，在递归的临界点存在一种简单情境，在这种简单情境下，我们应该直接给出问题的解决方案。一般地，在这种情境下，问题的解决方案是直观的、容易的。

（3）提取重复的逻辑，缩小问题规模。递归问题必须可以分解为若干个规模较小、与原问题形式相同的子问题，这些子问题可以用相同的解题思路来解决。从程序实现的角度而言，我们需要抽象出一个干净利落的重复的逻辑，以便使用相同的方式解决子问题。

3、递归算法的编程模型

在明确递归算法设计三要素后，接下来就需要着手开始编写具体的算法了。在编写算法时，通常有两种编码手法，两者本质上没有什么区别，只是解决问题的时机不同，如下所示：

模型一：在递去的过程中解决问题

function recursion(大规模)
{
if (end_condition) //明确的递归终止条件
{      
        end; //简单情景
}
else //在将问题转换为子问题的每一步，解决该步中剩余部分的问题
{ 
        solve;                // 递去
        recursion(小规模);     // 递到最深处后，不断地归来
    }
}

模型二：在归来的过程中解决问题

function recursion(大规模)
{
if (end_condition) //明确的递归终止条件
{
        end;  //简单情景
}
else // 先将问题全部描述展开，再由尽头“返回”依次解决每步中剩余部分的问题
{            
        recursion(小规模);     // 递去
        solve;                // 归来
    }
}

4、递归的应用场景

在我们实际学习工作中，递归算法一般用于解决三类问题：
（1）问题的定义是按递归定义的（Fibonacci函数，阶乘，…）；
（2）问题的解法是递归的（有些问题只能使用递归方法来解决，例如，汉诺塔问题，…）；
（3）数据结构是递归的（链表、树等的操作，包括树的遍历，树的深度，…）。

5、参考

本文部分内容参考自互联网