动态规划的递归写法和递推写法

动态规划是一种用来解决一类最优化问题的算法思想。简单来说，动态规划就是将一个复杂的问题分解成若干个子问题，通过综合子问题的最优解来得到原问题的最优解。动态规划会将每个求解过的子问题的解记录下来，这有当下一次碰到同样的子问题时，就可以直接使用之前的记录结果，提高了计算效率。一般可以使用递归或者递推的写法来实现动态规划，其中递归写法又称记忆化搜索。

1、动态规划的递归写法

在算法处理问题中，需要记录子问题的解，来避免下次遇到相同的子问题时的重复计算。例如，斐波那契数列的递归写法：

int F(int n){
    if(n == 0 || n == 1) return 1; 
    else return F(n - 1) + F(n - 2);
}

这会有很多重复的计算。为了避免重复计算，可以开一个一维数组temp，用来保存已经计算过的结果，其中temp[n]记录结果F[n]，并用temp[n] = -1来表示还没有被计算过。可以在递归中判断temp是否是-1，如果不是1，说明已经计算过temp[n],直接返回temp[n],就是结果，否则，按照递归形式进行递归。代码如下：

const int N = 1e5 + 7;
int temp[N];
int F(int n){
    if(n == 0 || n == 1) return 1;//递归边界
    if(temp[n] != -1) return temp[n];//已经计算过，直接返回结果，不再重复计算
    else{
        temp[n] = F[n - 1] + F[n - 2];//计算F[n]保存至temp[n]
        return temp[n];//返回F[n]的结果 
    } 
}

这样就把已经计算过的内容记录了下来，于是当下次再碰到需要计算相同的内容时，就可以直接用了，这也是记忆化搜索这个名字的由来。如图，记忆化搜索把时间复杂度从O（n2）降到了O（n），也就是说用一个O（n）的空间力量就让时间复杂度降低到了线性级别。

通过上面的例子可以引出一个概念：如果一个问题可以被分解成若干个子问题，且这些子问题会重复出现那就称这个问题有重叠子问题。动态规划通过记录重叠子问题的解来避免重复计算。因此，一个问题必须拥有重叠子问题，才能使用动态规划解决。

2、动态规划的递推写法

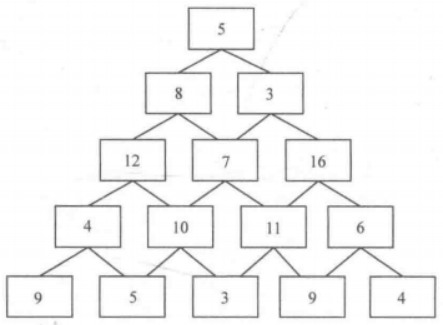
以数塔问题为例。将一些数字排成数塔状，其中第一层有一个数，第二层有两个数……第n层有n个数。现在要从第一层走到第n层，每次只能走向下一层链接的两个数字中的一个，问：最后路径上所有数字相加之后得到的最大和是多少？

#include<cstdio>
#include<algorithm>
#include<iostream>
using namespace std;
const int maxn = 100;
int n;
int f[maxn][maxn] = { 0 };
int temp[maxn][maxn] = { 0 };
int F(int i, int j)
{
    if (i == n)
    {
        temp[i][j] = f[i][j];
        return f[i][j];
    }
    temp[i][j] = max(F(i + 1, j), F(i + 1, j + 1)) + f[i][j];
    return  temp[i][j];
}
int main()
{
    cin >> n;
    for (int i = 1; i <= n; i++)        //输入树塔 
    {
        for (int j = 1; j <= i; j++)
        {
            cin >> f[i][j];
        }
    }
    //递归写法 ，将递推写法的代码屏蔽，直接调用F函数即可 
    //F(1,1);
    //递推写法 
    for (int j = 1; j <= n; j++)     //设置边界 
    {
        temp[n][j] = f[n][j];
    }
    //从第n层不断往上计算处temp[i][j]
    for (int i = n - 1; i >= 1; i--)
    {
        for (int j = 1; j <= i; j++)
        {
            //状态转移方程 
            temp[i][j] = max(temp[i + 1][j], temp[i + 1][j + 1]) + f[i][j];
        }
    }
    printf("%d", temp[1][1]);
}