第一节:一枚硬币的两面:指数爆炸与索引之快
1、折纸游戏
此为开篇之作,让我们来领略一下指数爆炸。请看下面的思考题:
假设现在有一张厚度为1mm的纸,纸质非常柔软,可以对折无数次。每对折1次,厚度便翻一番。已知地球距月球约39万公里,请问对折多少次后厚度能超过地月距离呢?
很多人会觉得这是一个非常大的数字,其实正确的答案是:39次
足够震撼吧!仅仅对折了39次,就让1mm的纸的厚度达到了地球到月球的距离,实在是让人大吃一惊!我们把这种数字急速增长的情况称为指数爆炸。之所以称为指数爆炸是因为折纸时厚度(2n) 的指数n就是对折次数。
为使大家直观地理解指数爆炸,我们来画个图。横轴表示对折次数,纵轴表示厚度。
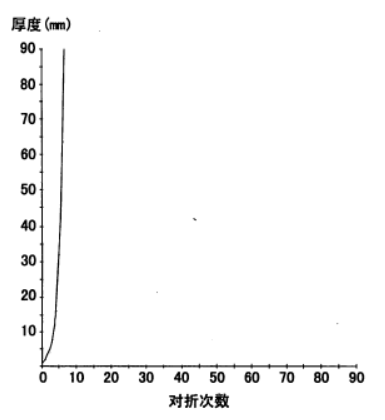
从图中可见,指数函数迅速攀升,其图像几乎垂直于x轴。
2、生日悖论
折纸游戏,略显无聊,谁没事去折纸玩呢!再来看一个与日常生活息息相关的现象吧:班级的人数达到多少人,至少有两个人同一天生日。所出现悖论的原因在于:这个问题的答案是一个很小的数值,让人吃惊。
正确的答案是:仅有64人的班级,至少有两个人的生日相同。
让我们看一些分析过程:

其中,n个人不同生日的概率为:
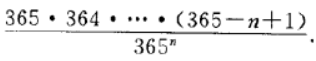
分母又是一个指数函数,将会变得巨大,其整体的值近似为0了。所以,当班级达到64人的时候,至少出现两个人生日的相同的概率将近1。
3、索引的秘密武器:二分法
指数大爆炸,让我们领略了指数增长的巨大爆发力。而二分查找则是指数大爆炸的反例,在巨大海量的数据中,它能让我们领略快速查找的巨大威力。这种威力是难以想象中的震撼。
例如数据库中的查找,如果不采用任何措施的话,看似简单的查找,往往都是全表扫描,速度那可真是龟速。也许你觉得这是危言耸听,感觉无所谓,自认为当前的CPU十分的强悍,抱着一切无所谓的态度。看看下面一组数据的对比,让你对龟速有个直观的体验吧:
在一个10000条记录的数据表中,查找一次平均需要5000次比较,而在使用了索引的表中只需要14次。
看到了吧,这是10000对14的对比,这就是二分查找的巨大威力所在。
作者寄语:本文希望通过三个例子,让大家直观的感受索引对查询的重要性。索引是极其重要的,并不是可有可无的东西。

mark 一下